Is faster than speed-of-light travel possible given the laws of relativity?
One of the postulates of special relativity is that photons (and actually all massless particles) travel at the speed of light, and a corollary of this postulate is that signals (consisting of either massless or massive information) cannot travel at speeds faster than light. Thus, according to relativity, the superluminal travel of signals is not possible.
This fact is often referred to as causality, and it is theoretically rendered by demanding that if event 1 causes event 2, then the time it takes for event 1 to cause event 2 is greater than or equal to the time it takes light to travel from event 1 to event 2. If this were not the case, then we could Lorentz boost to a frame where event 2 occurred before event 1.
However, causality does not absolutely forbid superluminal “travel” itself as long as said travel is not causal, and thus the key in applying the fundamental speed limit of nature is to recognize that the spacetime separation between non-causal events has no speed limit. Here, we give an example of this fact in which a wave seems to move faster than the speed of light, but whose travel actually follows from relativistically consistent Lorentz transformations.
Introduction
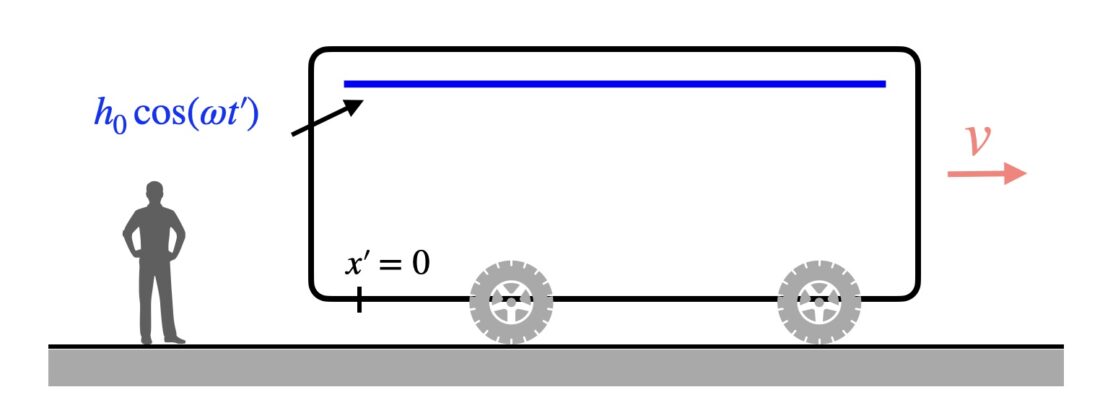
A long bar is on a train moving with speed \(v\). The bar lies with its axis parallel to the direction of motion of the train, and the entire bar undergoes simple harmonic motion with an amplitude \(h_0\), such that its height can be described by the equation
\begin{equation}
h(x’, t’) = h_0 \cos(\omega t’) \qquad (1)
\end{equation}
where \(x’\) is the horizontal position along the bar and \(t’\) is the time, both within the train frame (Figure 1).

(Figure 1: A long bar within a train undergoes simple harmonic motion within the train’s frame.)
However, from the perspective of someone on the ground, clocks that are within a moving frame and which are farthest away from the front of that frame (as defined by the direction of the frame’s velocity) are a constant time ahead of clocks closer to the front of the moving frame. David Morin mnemonically calls this the RCA or “rear-clock-ahead” effect and it more generally falls within the topic of the relativity of simultaneity. From within the train’s frame, both ends of the bar are at the same height at the same time, but this is not the case for someone outside the train frame.
Instead, from the ground frame we see the part of the bar at \(x’ = +\epsilon\) (for some small distance \(\epsilon\)) as slightly behind in time the part of the bar at \(x’ =0\). Thus if the point \(x’=0\) is at the highest height, then the point \(x’=+\epsilon\) is at some slightly lower height. Similar results apply all along the bar; a section of the bar at \(x\) is always seen at a time slightly behind the part at \(x-\epsilon\) and slightly ahead of the part at \(x+\epsilon\). Thus as we move to the right along the bar (again from the ground frame) the net effect of this lag (coupled with the oscillation of the bar itself) makes us see a wave.
Superluminal Wave Equation
Can we describe the seen wave with a wave equation? Yes!
Simply from the Lorentz transformation, we know that the time \(t’\) in the train frame can be written in terms of the \(t\) and \(x\) of the ground frame as
\begin{align}
t’ = \gamma( t – v x/c^2), \qquad (2)
\end{align}
where \(\gamma = \sqrt{1-v^2/c^2}\). Thus from the ground frame, the bar appears to act as a traveling wave (See Figure 2) defined by the equation
\begin{equation}
h(x’,t’) = h_0 \cos(\omega t’) = h_0 \cos(\omega\gamma( t- xv /c^2)) \equiv g(x, t). \qquad (3)
\label{eq:wav_soln}
\end{equation}

(Figure 2: From the ground frame the oscillating bar appears as a traveling wave)
Before we write the wave equation suggested by Eq.(3), let’s make some checks. What is the period and wavelength associated with the wave given by Eq.(3) and what do these values become in the non-relativistic limit \(v/c\to 0\)? From the form of the sinusoid itself, we find that the period and wavelength are, respectively,
\begin{equation}
T = \frac{2\pi}{\gamma \omega }, \qquad \lambda = \frac{2\pi c^2}{\gamma \omega v}.
\end{equation}
In the limit as \(v/c\to 0\), we find \(T\to 2\pi/\omega\) and \(\lambda \to \infty\) which are consistent with our expectations. Non-relativistically, we should not see any of the relativistic rear-clock-ahead effects, and should instead simply see a bar oscillating with period \(2\pi/\omega\). Such a bar could be interpreted as having an infinite wavelength and hence complete spatial uniformity.
OK back to finding the wave equation. From Eq.(3) we see that the equation \(g(x,t)\) satisfies the wave equation
\begin{equation}
\frac{\partial^2}{\partial t^2}g(x, t) = \frac{c^2}{v}\frac{\partial^2}{\partial x^2} g(x, t). \qquad (4)
\label{eq:wave_eqn}
\end{equation}
What does this equation suggest about the speed of our wave? From Eq.(4), we see the speed of the wave as seen from someone on the ground frame is
\begin{equation}
v_s = \frac{c^2}{v} = \frac{c}{v} \cdot c > c,
\end{equation}
suggesting that the wave is traveling faster than the speed of light. We seem to have violated a fundamental result of relativity and thus to have violated causality. What’s happening?
Causality Violated?
We recall that, as a shorthand, physicists define causality as the idea that physical signals (e.g., particles, information) cannot travel faster than the speed of light. However, above we obtained a wave equation that exhibited a speed that is faster than the speed of light. Have we shown that causality is violated in this system? Not quite.
The wave propagation observed by someone on the ground frame is a special relativistic effect and does not define a true dynamic process in which one part of the bar is pushing another part of the bar (as would occur with a wave on a string). There is no signal that is being transported from one end of the bar to the other, and so the peaks and troughs that seem to be moving faster than the speed of light do not define causally related phenomena. In essence, it is indeed possible to have two events that occur at times and distances that seem to suggest superluminal travel, as long as these two events are not causally linked.
Of course, we’re restricting ourselves to classical special relativity. Things, as always get stranger, when one incorporates quantum physics.